4次元に関する考察

　3次元空間において、その空間内に変化をもたらす為に必要な、逆行する事も、それどころかその方向を五感をもって認識する事さえも不可能な「時間」という概念が可逆となる事により、3次元空間に新たな方向への広がりが付加されたものが4次元時空である。

　この事から3次元存在と4次元存在の違いは以下の通り。

　・3次元存在は時間の流れを視認できないが、4次元存在にはそれが可能
　・3次元存在は時間軸を逆行できないが、4次元存在にはそれが可能

　しかし、私達の住む世界が3次元空間内である限り、4次元時空を正確に表現する事は不可能である。よって以下、3次元を1次元、4次元を2次元に例えて説明する事にする。


　【3次元存在は時間の流れを視認できない】

　3次元空間を直線からなる1次元世界に、3次元存在を1次元世界の中を移動できる点として置きかえる。この点が「移動できる」という事は「世界が変化している」ということであるから、この1次元世界には3次元世界同様に時間が流れているものとする。
　この「点」は過去を直接見る事は出来ない。自分が過去に居た位置を見る事は出来るが、そこに居た自分を見る事は出来ない。記憶・経験としてその過去の存在を知っている。未来もいずれ現在へと置き換わるであろう事を知っている。だが、直接見れるのは「現在」という刹那に限られる。
　つまりこの1次元存在には現実に自身の移動という変化を知る事は可能だが、その過程を「同時」に視認する事は不可能である。
　これが3次元存在にも言えるという事は言うまでも無いだろう。理由は本編でも述べられていたように、n次元存在は（n-1）次元の視界しか持たない為。
　4次元時空が3次元空間に時間という広がりを加えた物であるからには、その断片である3次元空間自体には時間の流れは存在しない。変化するには時間の流れが存在しなければならない。だから自身の変化の過程を示す「線」を3次元存在は見る事ができない。

　ここで注意しなければならないのは、今述べた「線」がx軸に平行な線ではないという事である。確かに「点」はx軸のみで構成される1次元世界の線上を移動する為、その軌跡もx軸に重なる物だと思われるかもしれない。だが、前述の「軌跡」とは移動と時間の経過を併せて考えた「変化」の軌跡である為、単に「点」の「移動」の軌跡の事を述べているわけではない。
　では、前者を描く為にはどうすれば良いか。変化の軌跡とはつまり、3次元存在でいうなら4次元時空から見下ろした際に見る事が出来る、彼が描いた軌跡という事になる。
　よって、1次元存在の変化の軌跡を描く為には新たにy軸を増やした平面上で表現する必要がある。


　【4次元存在は時間の流れを視認できる】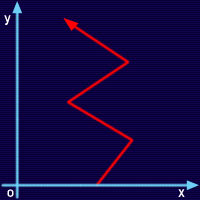

図1　ある平面におけるy軸方向の広がりを時間軸とし、x軸と平行になる直線を1次元世界全体の「現在」という刹那を切り出した断片と仮定する。つまりこの中に時間の流れは存在しない。
　そして1次元世界における時間の流れは、直線がy軸に直交するカタチで上へ上へと積み重なる事によって表現する。
　要するにダイヤグラムのような物だと考えるとわかりやすいかもしれない。この平面上で「点」が描く軌跡たる「線」こそが時間と位置を併せて見た「変化」の軌跡となる。
　先に述べたように「点」自身にはこの「線」を見る事が出来ない。それが可能なのはひとつ上の次元である2次元存在、つまり「面」という事になる。それが「点」の移動という変化を「同時」に視認した結果がこの「線」という事になる。
　無論視界は（n-1）次元であるから基本的には線のジグザクを認識できないが、これは3次元存在同様に複数の視点を持ったり視点を移動させたりする事によって擬似的に認識できるようになる。
　この図ではジグザグを俯瞰できるが、それは私達が完全な2次元視界を持つからであって、2次元存在の視点からはこのようには見えない。実際には俳句のパスワードを見るシーンでの、ギリギリまで傾けた画像のように見えると思われる。


【3次元存在は時間軸を逆行できない】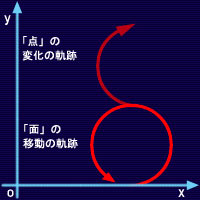

図2 　さて、この平面上に描かれる線が、例えば「O」のようなカタチを描く事は無い。1次元存在がそのような軌跡を描こうと試みても「S」になってしまう。右から左へ、中央に達してから更に左へ移動し右へ戻ろうとしてもy軸方向へ逆行出来ない為である。覆水盆に帰らず。SはOにならず。
　対して始めから平面上に存在する2次元存在ならば1次元存在にとっては不可逆なy軸を逆行できるので「O」の軌跡を描く事が可能である。
　つまり「点」にとっては不可逆であるところの時間の流れを逆行する事が可能である事を意味する。
　ただし、こちらは「変化」の軌跡ではなくて「移動」の軌跡である。2次元存在の変化の軌跡はこの図では表す事はできない。






　ここまで長々と1次元の移動体である「点」と2次元の移動体である「面」の違いを述べてきたが、なぜこの両者に例えたのかというと、もう1次元上を残しておけば後で並列世界に関しても説明しやすいからである。
　しかし、長くなってしまったのでこちらは次回にまわす事にする。


戻る